La mesure des distances, des angles et du temps
François Desvallées
Les distances
| Les unités | ||
| La mesure de la Terre | 10000km | 107m |
| La Lune et le Soleil | millions de km | 109m |
| Le Système solaire | milliards de km | 1012m |
| 1 année lumière | 10 000 milliards de km | 1016m |
| Notre galaxie | 100000 années lumière | 1021m |
| Les autres galaxies | millions d’années lumière | 1022m |
| L’Univers observable | milliards d’années lumière | 1026m |
##Les unités de distance
| Antiquité | pied, coudée, stade, farasange, … |
| Autres | farsakh, verste, li, … |
| Système Impérial | pouce, pied, yard, mille, … |
| Système métrique | .. |
##Définition du mètre
| 1793 | Dix-millionième du quart du méridien terrestre |
| 1889 | Mètre étalon en platine iridié |
| 1960 | 1650763.73 longueurs d’onde de la ligne orange/rouge du krypton 86 |
| 1983 | Distance parcourue par la lumière en 1/299792458 seconde |
Mesurer les distances sur la Terre: la triangulation
Si on connaît un côté d’un triangle et deux de ses angles, on connaît tout 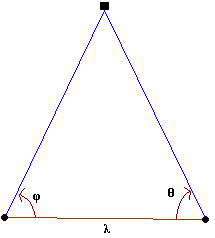


Triangulation - les méridiennes
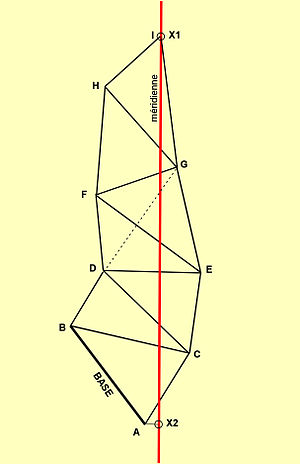

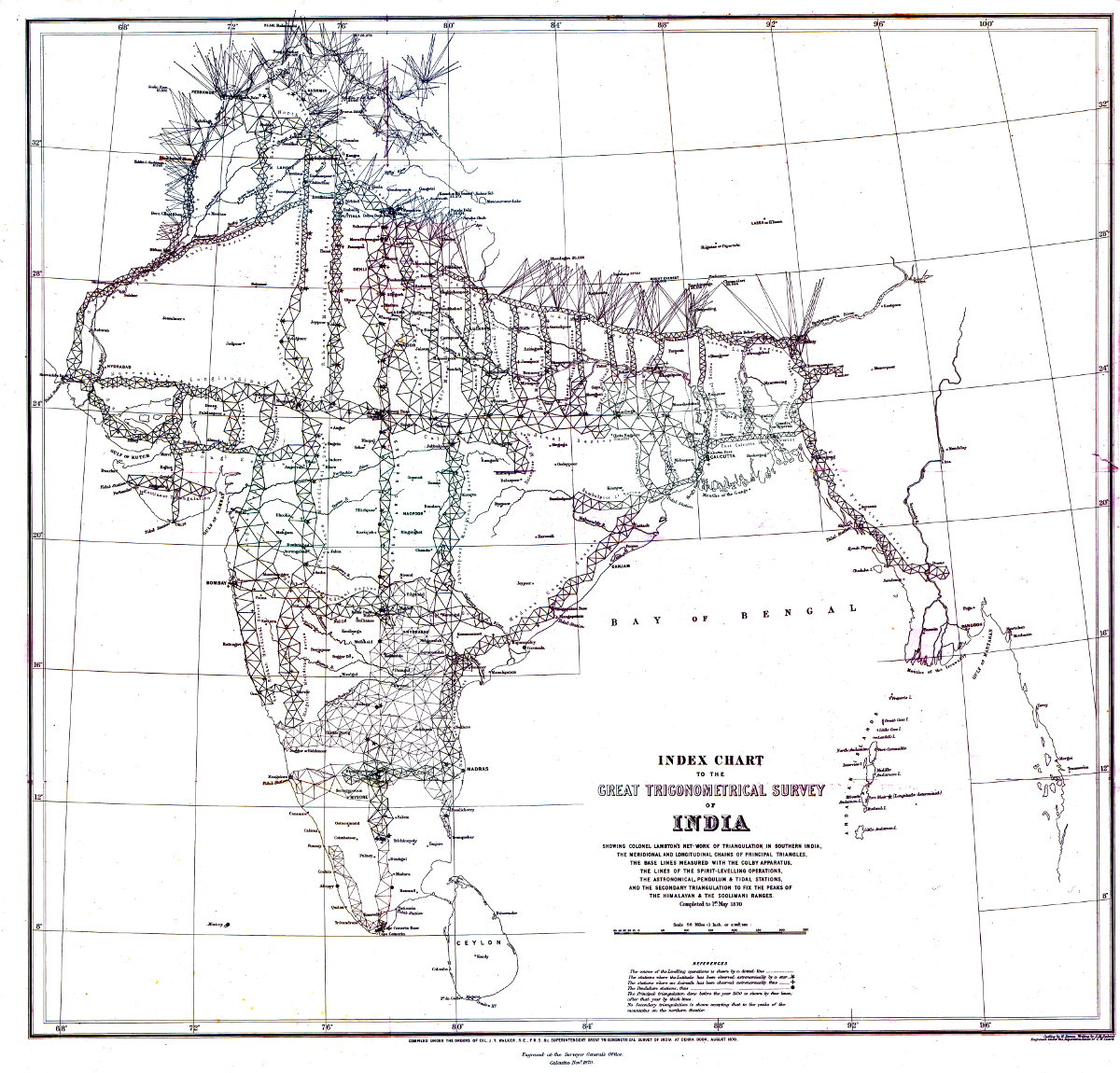
La mesure de la Terre
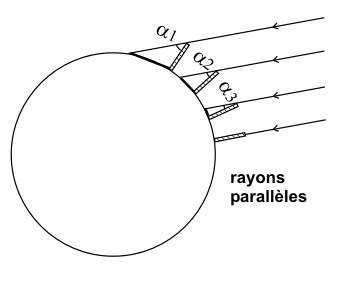
A première vue, la Terre est plate et l’Univers est infini. Les Grecs savaient que la Terre est ronde, mais ne connaissaient pas sa taille, jusqu’à Eratosthène qui a obtenu un très bon résultat avec sa mesure de l’ombre d’un obélisque.
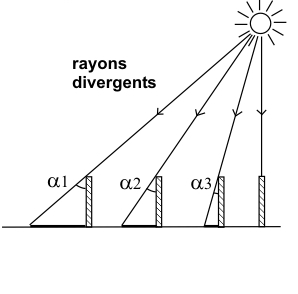
La Lune
Si on connaît la taille de la Terre, on peut trouver la taille et la distance de la Lune (en mesurant l’ombre de la Terre lors des éclipses de Lune), et sa distance (par trigonométrie)

Le Soleil
Aristarque de Samos a obtenu une (mauvaise) estimation de la taille et de la distance du Soleil.
Le Système Solaire
Au XVII° siècle Képler a déterminé les orbites et les lois qui régissent ces mouvements,

puis Newton les a expliquées et mises en équations, mais toujours sans connaître la distance Terre-Soleil (Unité Astronomique) 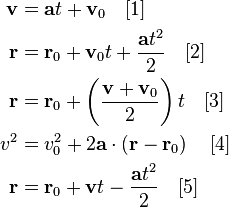

Depuis Képler on savait que le rayon de l’orbite de Jupiter était d’environ 5 UA. Mais combien vaut une UA en kilomètres?
Les transits de Mercure et Vénus ont donné des résultats, mais ceux-ci restaient imprécis à cause des erreurs dûes à l’atmosphère.
Ce n’est que vers 1960 que des mesures par radar de Vénus ont donné la mesure de l’UA avec une bonne précision (149 597 870 km).
Les étoiles proches
L’UA est l’échelle pour mesurer tout le système solaire et les distances aux étoiles proches, grâce à la parallaxe (que nous utilisons aussi pour notre vision binoculaire).
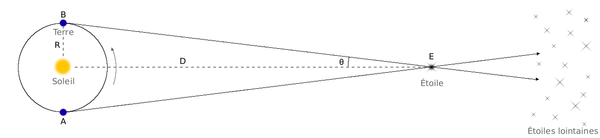
La première mesure de distance d’étoiles par parallaxe (en 1860) a été réalisée sur 61 Cyg: 720 000 UA = 11,4 AL.
Les étoiles lointaines
Pour les étoiles plus lointaines, on utilise une autre méthode: L’éclat apparent dépend de la luminosité absolue et de la distance.
Si on connaît la luminosité on peut trouver la distance.
On peut estimer la luminosité absolue grace à la spectroscopie, mais aussi aux “bougies étalons” (standard candles)
Les Céphéides

Henrietta Leavitt

Les galaxies et autres objets lointains
C’est Edwin Hubble au début du XXe siècle qui a bouleversé notre connaissance de l’Univers, par l’étude des céphéides de M31 et du décalage vers le rouge (red shift), en montrant que la vitesse d’éloignement des galaxies est proportionnelle à leur distance.
GN-z11 : 13.39 milliards d’années lumière


La mesure des angles
Unités
Systèmes de coordonnées
Instruments
Astrométrie
Les unités
Le même angle exprimé en..
| Radians | Degrés sexagésimaux | Degrés décimaux | Ascension droite |
|---|---|---|---|
| 0.2618 | 15° | 15.0° | 1h |
| 1 | 57°17’44" | 57.2958° | 3h49m11s |
| 2π | 360° | 360.0° | 24h |
Systèmes de coordonnées

Azimut (A)
Altitude (a)

Ascension droite (α)
Déclinaison (δ)
Coordonnées terrestres et célestes
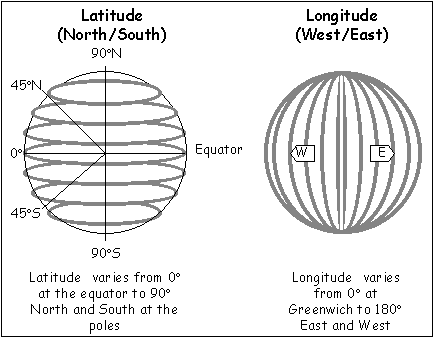
| Direction | Nord - Sud | Est - Ouest |
|---|---|---|
| Terre | Latitude (φ) | Longitude (λ) |
| Ciel | Déclinaison (δ) | Ascension droite (α) |
Conversions de coordonnées
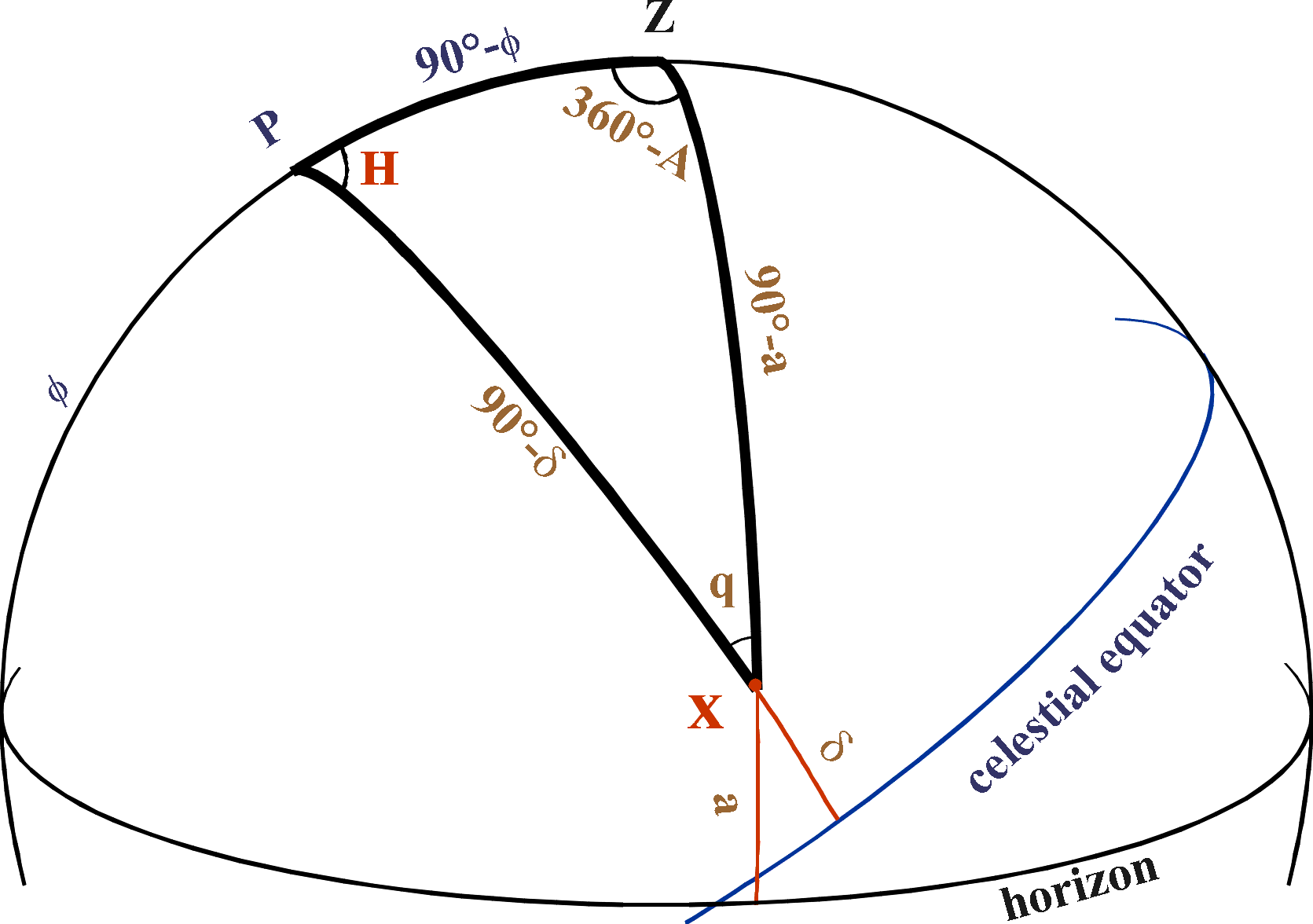
- H = t - α
- sin(a) = sin(δ) sin(φ) + cos(δ) cos(φ) cos(H)
- sin(A) = - sin(H) cos(δ) / cos(a)
- cos(A) = { sin(δ) - sin(φ) sin(a) } / cos(φ) cos(a)
Les instruments de mesure d’angles: Quadrants et Sextants

Astrolabe

Armilles

L’observatoire d’Ulug Begh


Lunettes méridiennes


L’astrophotographie
 James Abell au Big Schmidt du mont Palomar
James Abell au Big Schmidt du mont Palomar

Gaia


Orbite de Gaia
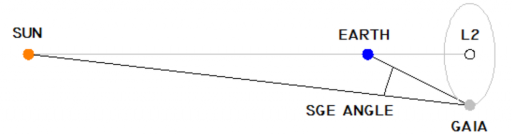
Le point L2 est à 1,5 million de kilomètres
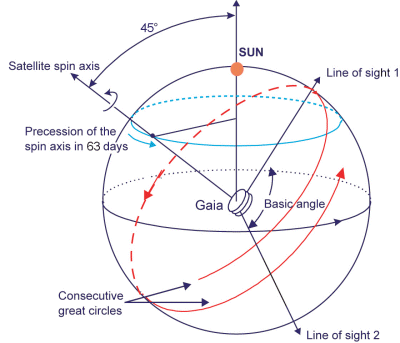 Gaia tourne sur lui-même en 6 heures
Gaia tourne sur lui-même en 6 heures
Le temps
Temps local apparent
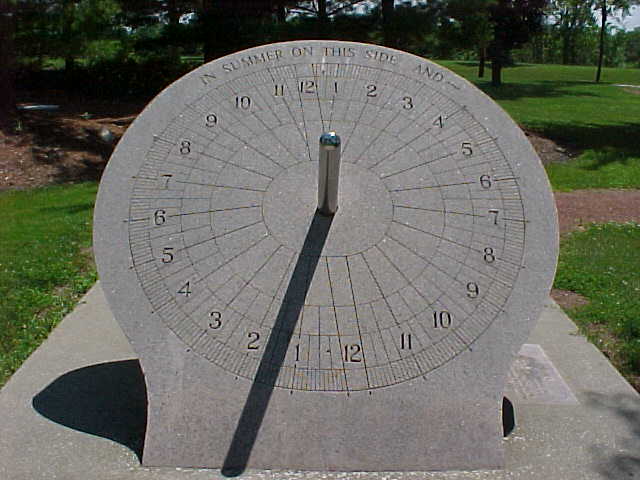
Analemme

Temps relatif à la rotation de la Terre
| Temps local apparent | Rotation de la Terre par rapport au Soleil |
| Temps solaire moyen | “Soleil moyen” - corrige les irrégularités |
| Temps universel | TU - anciennement GMT - défini au méridien de Greenwich |
| Temps sidéral | Rotation de la Terre par rapport aux étoiles |
Temps uniforme
| Temps atomique international | moyenne de 200 horloges atomiques |
| Temps coordonné géocentrique | au centre de la Terre |
| Temps coordonné barycentrique | au centre du Soleil |
Le mois
| Mois sidéral | Période orbitale de la Lune |
| Mois synodique | Intervalle entre deux nouvelles lunes consécutives |
| Mois anomalistique | Intervalle de temps entre deux périgées de la Lune |
| Mois tropique | Temps mis par la Lune pour retrouver la même longitude écliptique |
| Mois draconitique | Période entre deux passages de la Lune au même nœud de son orbite |
Dans les calendriers lunaires ou lunisolaire, un mois lunaire correspond à deux alignements successifs du Soleil, de la Terre et de la Lune
(syzygies identiques!!).
Clepsydres et sabliers

Christiaan Huygens - 1657

Navigation
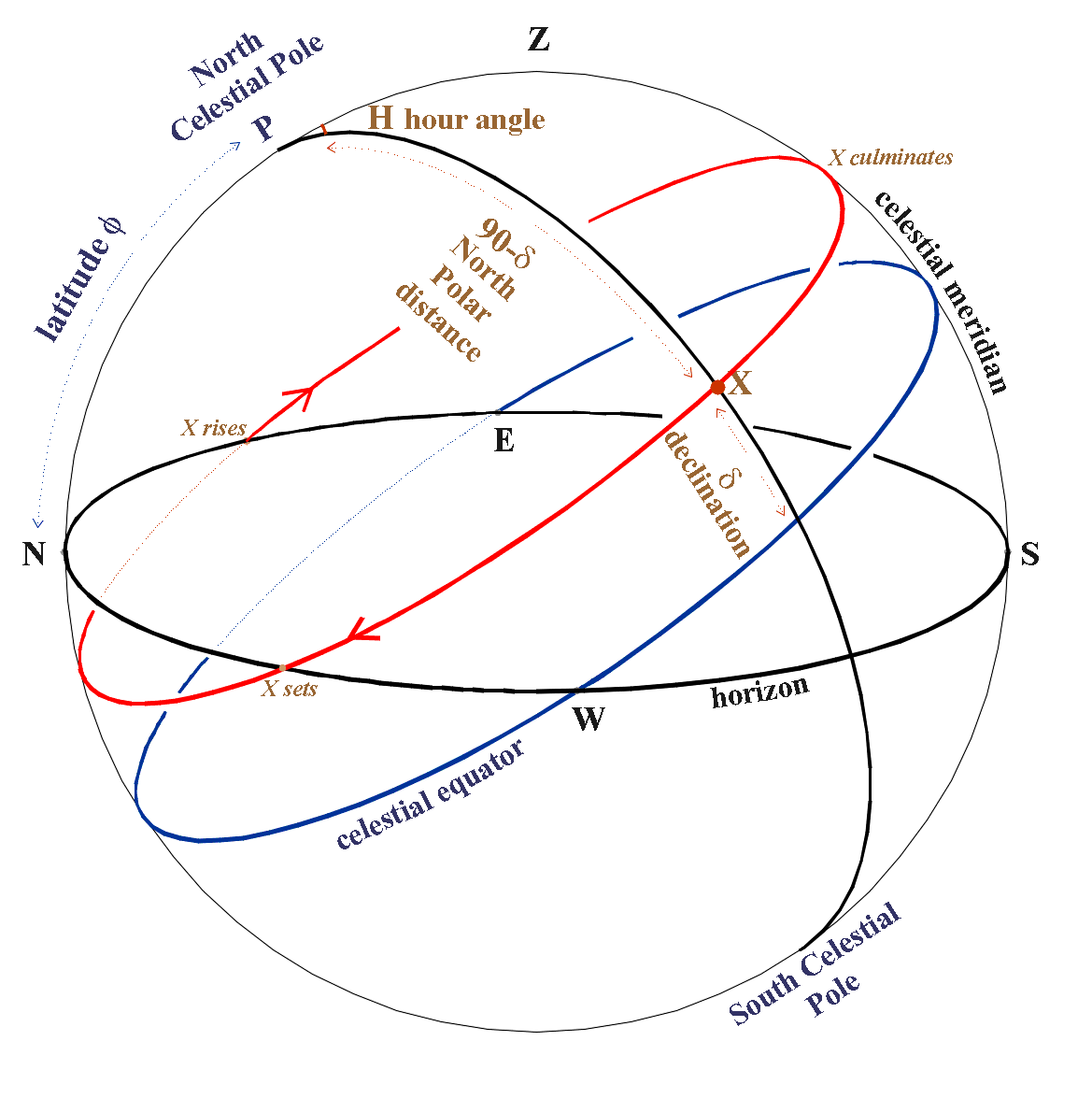
En observant le passage au méridien d’un astre:
- il est facile de trouver la latitude
- si on connaît l’heure, on peut en déduire la longitude
Jusqu’à l’invention d’horloges précises, on ne pouvait pas établir correctement sa longitude
Horloge de John Harrison - 1725


Horloges à quartz

Horloges atomiques

GPS - Global Positioning System
Références
Crash Course Astronomy - Phil Plait
The Astronomical Companion - Guy Ottewell
Astronomie Générale - André Danjon
The Exact Sciences in Antiquity - Otto Neugebauer